- Paraboloïde hyperbolique
-
● Paraboloïde hyperbolique quadrique d'équation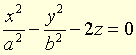 .
.
Encyclopédie Universelle. 2012.
● Paraboloïde hyperbolique quadrique d'équation
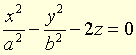 .
.Encyclopédie Universelle. 2012.
Paraboloïde hyperbolique — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
paraboloïde — [ parabɔlɔid ] n. m. • 1691; adj. 1660 ; de 2. parabole ♦ Géom. Quadrique n ayant pas de centre. Paraboloïde elliptique, hyperbolique, dont certaines sections planes sont des ellipses, des hyperboles. Paraboloïde de révolution : surface engendrée … Encyclopédie Universelle
Paraboloide — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
Paraboloïde circulaire — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
Paraboloïde elliptique — Paraboloïde En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un… … Wikipédia en Français
hyperbolique — [ ipɛrbɔlik ] adj. • 1541; lat. hyperbolicus, gr. huperbolikos I ♦ Rhét. Caractérisé par l hyperbole. Style hyperbolique. Cour. Des compliments hyperboliques. ⇒ emphatique, grandiloquent. Philos. Le doute hyperbolique (Descartes). II ♦ (1646) 1 ♦ … Encyclopédie Universelle
Paraboloïde — En mathématiques, un paraboloïde est une surface du second degré de l espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie. Certaines sections d un paraboloïde avec un … Wikipédia en Français
paraboloïde — (pa ra bo lo i d ) s. m. 1° Terme de géométrie. Surface du deuxième degré dépourvue de centre. On distingue deux sortes de paraboloïdes : le paraboloïde elliptique, qui est composé d une seule nappe infinie ; et le paraboloïde hyperbolique qui… … Dictionnaire de la Langue Française d'Émile Littré
QUADRIQUES — Les surfaces de l’espace matériel, que nous connaissons par leur emploi, en architecture par exemple, étaient autrefois classées en «corps ronds» et «corps droits». La sphère et le cube sont des surfaces typiques de ces deux familles. Les corps… … Encyclopédie Universelle
Quadrique — En mathématiques, et plus précisément en géométrie euclidienne, une quadrique, ou surface quadratique, est une surface de l espace euclidien de dimension 3, lieu des points vérifiant une équation cartésienne de degré 2 Ax2 + By2 + Cz2 + 2Dyz +… … Wikipédia en Français